Hello Julio,
I am confused about the duration approximation, especially your solution for Q1 - c.
The formula given in the formula sheet is: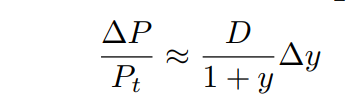
Which I believe this is correct, as modified duration behaves much like an “elasticity” of the bond’s price with respect to its yield—with one key distinction: we treat changes in yield as absolute decimal changes (i.e., changes in percentage points), rather than proportional changes in the yield itself.
However, the solution presented uses an approach that does not make sense to me. First, it employs the normal Macaulay duration (1.95) instead of the modified duration (1.81). Then it treats the absolute price change (+5) as if it were the percentage price change (+5.26 %).
I believe the correct approach would reflect a 2.9 percentage‐point decrease in yield, yielding a final YTM of approximately 4.89 %.
The fact that their result is close to the “true” answer is purely coincidental—here, +5 € is numerically similar to +5.26 %. Under different circumstances (other prices or durations), that coincidence would disappear and lead to a larger discrepancy.