Maybe this way us better for me to explain my doubt:
b)
me: PV=(200/0,4%)*(1-1/(1+0,4%))^11*1) => FV= PV*(1+0,4%)^11
solutions: PV=(200/0,4%)*(1-1/(1+0,4%))^11*1)=> FV= PV*(1+0,4%)^11 => FV=PV*(1+0,4%)^11
Here we are doing the same thing with PV, I use T=11 (already accounting for the "start 2 months from now")
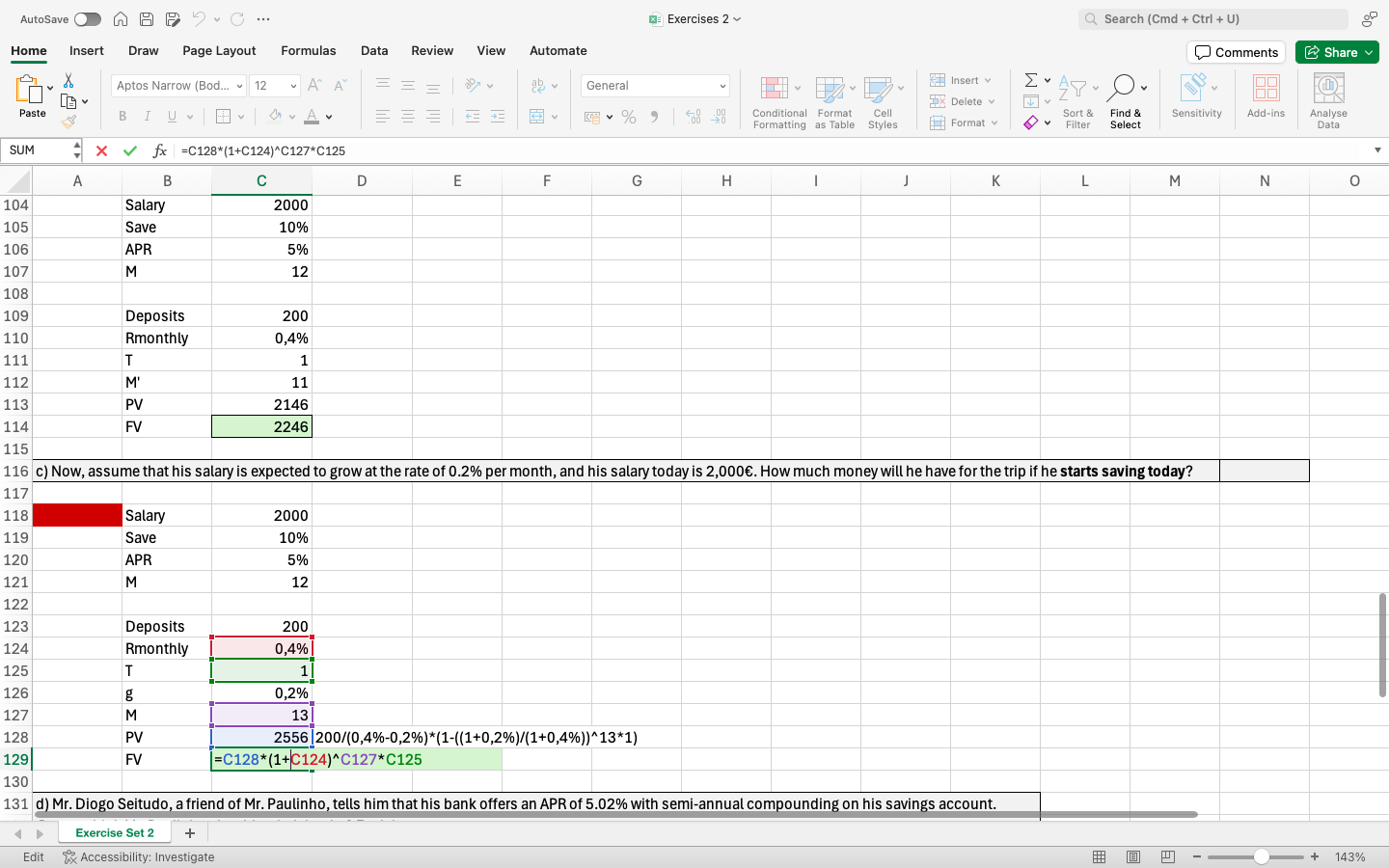
c)
me: PV= 200/(0,4%-0,2%)*(1-((1+0,2%)/(1+0,4%))^13*1) => FV =PV*(1+0,4%)^13
solutions: PV= 200/(0,4%-0,2%)*(1-((1+0,2%)/(1+0,4%))^13*1)*(1+0,4%) => FV= PV*(1+0,4%)^12
Here I would be expecting the same logic: since saving are starting today, T=13
As we already account for starting now (As we use T=13),, I don't understand why we multiply the value by (1+0,4%). In my point of view, that would be done only when computing FV.