Doubts

Mock Midterm - Q3

Mock Midterm - Q3

by Margarida Rei Parreira Dias -
Number of replies: 2

Dear professor, 

I am not understanding how do we go from this 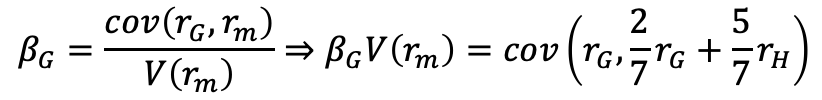to this 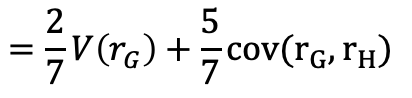, as I am not understanding how to separate the covariance into the variance of rg and the covariance of rg,rh.


Moreover, on that same exercise, I am not understanding how do I get here: 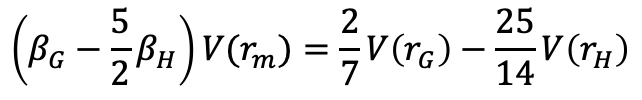. Could you help me, please?


Thank you and kind regards!

In reply to Margarida Rei Parreira Dias

Re: Mock Midterm - Q3

by Julio Crego -

No problem, Let's start with the first question.

First, I use that the covariance of a sum is the sum of covariances:

\(cov(r_G,\dfrac{2}{7}r_G+\dfrac{5}{7}r_H)=cov(r_G,\dfrac{2}{7}r_G)+cov(r_G,\dfrac{5}{7}r_H)\)

Now I use the fact that non-random variables can "leave" the covariance \(Cov(x,ay)=aCov(x,y)\)

\(cov(r_G,\dfrac{2}{7}r_G)+cov(r_G,\dfrac{5}{7}r_H)=\dfrac{2}{7}cov(r_G,r_G)+\dfrac{5}{7}cov(r_G,r_H)\)

Finally, I use that the covariance with itself is the variance \(cov(x,x)=V(x)\)

\(\dfrac{2}{7}cov(r_G,r_G)+\dfrac{5}{7}cov(r_G,r_H) = \dfrac{2}{7}V(r_G)+\dfrac{5}{7}cov(r_G,r_H)\)
In reply to Margarida Rei Parreira Dias

Re: Mock Midterm - Q3

by Julio Crego -
The second question. We have:

\(\beta_GV(r_m) = \dfrac{2}{7}V(r_G) + \dfrac{5}{7}cov(r_G,r_H)\)
\(\beta_HV(r_m) = \dfrac{5}{7}V(r_H) + \dfrac{2}{7}cov(r_G,r_H)\)

Now I will leave the first equation as it is and multiply the second by \dfrac{5}{2}

\(\beta_GV(r_m) = \dfrac{2}{7}V(r_G) + \dfrac{5}{7}cov(r_G,r_H)\)
\(\dfrac{5}{2}\beta_HV(r_m) = \dfrac{25}{14}V(r_H) + \dfrac{5}{7}cov(r_G,r_H)\)

Finally, I subtract the second equation from the first. Note how the covariance term disappears

\(\beta_G V(r_m)-\dfrac{5}{2}\beta_H V(r_m) = \dfrac{2}{7} V(r_G)-\dfrac{25}{4} V(r_H)\)